Apprendre le langage binaire

Bienvenue dans notre série de 6 vidéos, sur le langage binaire ! Dans cette première vidéo, nous allons découvrir ce qu’est le langage binaire et pourquoi il est essentiel en informatique.


Langage binaire
Durée : 13 mn 37

Les Nombres en Binaire
Durée : 22 mn 28

Les Caractères en Binaire
Durée : 8 mn 45

Binaire dans l'Informatique Moderne
Durée : 8 mn 45

Applications Pratiques du Langage Binaire
Durée : 9 mn 36

Conclusion & Ressources
Durée : 8 mn 40

En haut

Introduction au langage Binaire

Système binaire

Le langage binaire repose sur le système binaire, qui vient de la contraction de l’expression “binary digit”, on nomme couramment bit de l'anglais binary , soit « chiffre binaire » et qui utilise seulement deux chiffres : 0 et 1. C'est très différent du système décimal, qui lui est sur 10 chiffres : 0 1 2 3 4 5 6 7 8 9, que nous utilisons au quotidien. Voyons pourquoi le binaire est essentiel en informatique. C'est comme un langage secret pour les ordinateurs. Je vais vous montrez comment cela fonctionne dans plusieurs vidéos, car mettre tout dans une seule et même vidéo ce serais trop long et je risque de vous perdre en cours de route.

Définition des bits et des octets.

Pour comprendre le binaire, il est essentiel de connaître les unités de base : les bits et les octets. Un bit est le plus petit élément du binaire, il peut être soit 0, soit 1. Et un octet est composé de 8 bits.

Si on voulais vulgarisé et imagé mes propos, le “0” binaire pourrais être comparer à une lampe de bureau éteint ; quand au “1” binaire, serais la lampe du bureau allumé. Quand à l’octet, il a une valeur numérique de 1 à 255, soit un caractère d’un texte.

Conversion Binaire en Décimal

Exemples pratiques.

Maintenant que nous comprenons les bases, explorons comment convertir un nombre binaire en décimal. Prenons l'exemple du nombre binaire 1101, qui équivaut au chiffre 13 en décimal.

Voici comment nous pouvons convertir ces chiffres...

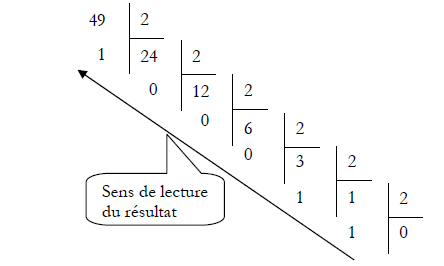
Il faut effectuer des divisions entières successives du nombre décimal par la base d’arrivée, qui est le binaire dans notre exemple et ce jusqu’à obtenir un quotient nul. Le 1er reste obtenu correspond à la base 2.

Pour mettre en pratique ce que nous avons appris, nous allons décoder un message binaire. C'est plus facile que vous ne le pensez. Restez avec moi ! Je vous mettrais sur mon site le tableau, et vous pourrez le recopier et complété si cela vous intéresse.

Conclusion

Dans cette première vidéo. Nous avons posé les fondations du langage binaire. Dans la prochaine vidéo, nous approfondirons notre compréhension en explorant la représentation des nombres en binaire. Assurez vous de vous abonner pour ne pas manquer la suite passionnante de cette série !

La Représentation des Nombres en Binaire

Introduction - Représentation des Nombres

Bienvenue pour la deuxième vidéo de notre série sur le langage binaire. Aujourd'hui, nous allons explorer la manière dont les nombres sont représentés en binaire.

Comment les nombres sont représentés en binaire.

Le binaire nous permet d'effectuer des opérations de base telles que l'addition, la soustraction, la multiplication et la division ; tout comme le décimale. Voyons comment réaliser ces opérations...

Notion de poids des chiffres binaires.

Prenons des exemples concrets pour voir comment les opérations binaires fonctionnent. Vous serez surpris de voir à quel point cela peut être simple !

Les addition dans le binaire, il faut retenir 0 + 0 cela fait 0, 0 + 1 ou 1 + 1 cela feras toujours 1.

Les soustraction dans le binaire, il faut retenir 0 - 0 cela fait 0, 0 - 1 et on retient 1 ou 1 - 1 cela feras toujours 1.

Pour illustrer nos concepts, prenons quelques exemples pratiques. Additions, soustractions, multiplions et divisons des nombres binaires.

Conclusion

C'est tout pour cette deuxième vidéo. Nous avons exploré la représentation des nombres en binaire et les opérations de base. Dans notre prochaine vidéo, nous verrons comment les lettres et les caractères sont représentés en binaire. N'oubliez pas de vous abonner pour ne rien manquer !

Les Lettres et les Caractères en Binaire

Introduction - les lettres dans le binaire

Bienvenue dans la troisième vidéo de notre série sur le langage binaire pour les novices. Aujourd'hui, nous allons découvrir comment les lettres et les caractères sont représentés en binaire.

Représentation des Lettres

Les ordinateurs utilisent le binaire pour représenter toutes les lettres et les caractères que nous utilisons. Nous allons explorer comment cela fonctionne.

Présenter le tableau entre les lettres de l’alphabet et le code binaire.

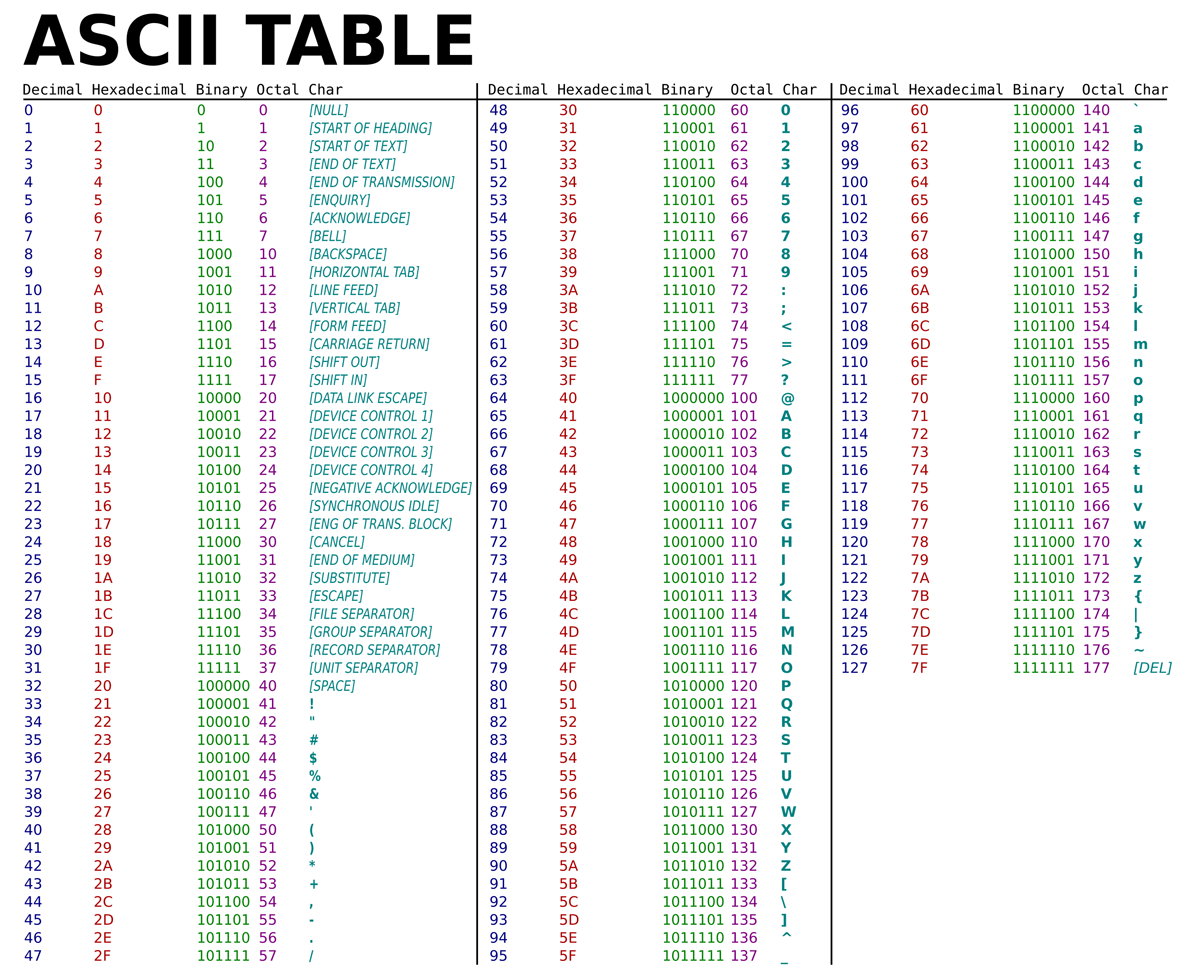
Encodage de Texte

Découvrons comment encoder un message en binaire. C'est ce qui se passe lorsque vous envoyez un message sur votre ordinateur ou téléphone.

Exemple Pratique ; Pour que tout soit clair, nous allons encoder et décoder un message en binaire. Vous verrez à quel point c'est fascinant et utile !

Bienvenue sur ma chaîne les tutoriels d'enrico 78. - 01000010 01101001 01100101 01101110 01110110 01100101 01101110 01110101 01100101 00100000 01110011 01110101 01110010 00100000 01101101 01100001 00100000 01100011 01101000 01100001 11000011 10101110 01101110 01100101 00100000 01101100 01100101 01110011 00100000 01110100 01110101 01110100 01101111 01110010 01101001 01100101 01101100 01110011 00100000 01100100 00100111 01100101 01101110 01110010 01101001 01100011 01101111 00100000 00110111 00111000 00101110

Conclusion

Bravo pour avoir atteint la fin de cette troisième vidéo. Vous comprenez déjà comment les lettres et les caractères sont gérés en binaire. Dans notre prochaine vidéo, nous verrons comment le binaire est utilisé dans l'informatique moderne. N'oubliez pas de vous abonner pour la suite passionnante !

L'Utilisation du Binaire dans l'Informatique Moderne

Introduction

Bonjour à toutes et à tous, bienvenue dans la quatrième vidéo de notre série sur le langage binaire. Aujourd'hui, nous allons découvrir comment le binaire est utilisé dans l'informatique moderne.

Les ordinateurs utilisent le binaire pour stocker toutes sortes de données. Voyons comment cela fonctionne et pourquoi c'est crucial.

représenté des schémas et autres images

Communication en Réseau

Le binaire est également utilisé pour la communication en réseau. C'est ce qui permet à Internet de fonctionner. Explorons cette technologie.

Conclusion

Félicitations pour avoir suivi cette série sur le binaire pour les novices jusqu'ici. Vous avez désormais une compréhension solide de son importance. Restez avec nous pour plus de contenus à venir !

Applications Pratiques du Langage Binaire

Introduction

Bienvenue dans la cinquième vidéo de notre série sur le langage binaire. Aujourd'hui, nous allons découvrir quels sont les applications binaire qui sont utilisé dans l'informatique.

Conclusion

Félicitations pour avoir suivi cette série sur le binaire pour les novices jusqu'ici et vous arrivez sur l'avant dernière de cette série. Vous avez désormais une compréhension solide de son importance. Restez avec nous pour plus de contenus à venir !

Conclusion et Ressources Supplémentaires

Introduction

Bienvenue dans la sixième et dernière vidéo de notre série sur le langage binaire. Aujourd'hui, nous allons faire un résumé de tout ce l’on a découvert dans le monde du binaire et l’utilisé dans l'informatique.

Ressources pour Aller Plus Loin


Quiz et/ou question

Conclusion

Félicitations pour avoir suivi cette série sur le binaire pour les novices jusqu'ici et vous arrivez sur la fin de cette série. Vous avez désormais une compréhension solide de son importance. Restez avec nous pour plus de contenus à venir !